1.4. Ratios, Rates, and Percent

Ratios and Rates

Ratio: a relationship between two numbers, expressed as a quotient with the same unit in the denominator and the numerator. There are three ways to write a ratio.

The ratio of a and b is:     a to b      or      a : b      or      \frac{a}{b}

Example:  Write the ratio of 5 cents to 9 cents.

5 to 9      or      5 : 9      or      \frac{5}{9}

 

  • Write a ratio in lowest terms (simplify):

– Write the ratio in a fractional form.

– Simplify and drop the units if given (as they cancel each other out).

Example:       4 : 28 = \frac{\bcancel{4}}{\bcancel{28}}=\frac{1}{7}

  \div4

    

Example:       0.75 metres to 0.25 metres       \frac{0.75m}{0.25m}=\frac{\bcancel{75}}{\bcancel{25}}=\frac{3}{1}=3

     \times100    \div25

 

Rate: a ratio of two quantities with different units.

Example:  teachers to students;   money to time;   distance to time, etc.

\frac{2\;teachers}{83\;students}   ,   \frac{24\;dollars}{3\;hours}   ,   \frac{85\;miles}{2\;hours}

  • Write a rate in lowest terms (simplify the rate):

Example:  80 kilometres per 320 minutes:       \frac{\bcancel{80}km}{\bcancel{320}min}=\frac{1km}{4min}

÷80

 

Unit rate: a rate in which the number in the denominator is 1.

Example:  15 dollars per hour:            \frac{\$15}{1h} = $15/h
  • Some unit rates:

– Miles (or kilometres) per hour (or minute).

– Cost (dollars/cents) per item or quantity.

– Earnings (dollars) per hour (or week).

Proportion: an equation with a ratio (or rate) on two sides (\frac{a}{b}=\frac{c}{d}), in which the two ratios are equal.

 Example:  Write the following sentence as a proportion.

3 printers is to 18 computers as 2 printers is to 12 computers.

\frac{3\;printers}{18\;computers}=\frac{2\;printers}{12\;computers}

 

Solving a proportion:

  • Cross multiply: multiply along two diagonals.     \frac{a}{b}=\frac{c}{d}
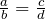
  • Solve for the unknown.

 

Example 1.4.1

4 litres of milk cost $4.38. What is the cost of 2 litres?

  • Facts and unknown:
4 L milk 2 L milk
$4.38 $ x = ?
  • Proportion:
 \frac{4\;L}{\$4.38}=\frac{2\;L}{\$x}
  • Cross multiply:
 (4)(x)=(2)(4.38)
  • Solve for x:
 \frac{\bcancel{4}x}{\bcancel{4}}=\frac{2(4.38)}{4} Divide both sides by 4.
x=\frac{(2)(4.38)}{4}=2.19
2 litres of milk cost $2.19.
  • Check:
 \frac{4\;L}{\$4.38}=\frac{2\;L}{\$2.19} Replace x with 2.19.
(4) (2.19) = (2) (4.38)
8.76 = 8.76 Correct!

 

Example 1.4.2

Tom’s height is 1.75 metres, and his shadow is 1.09 metres long. A building’s shadow is 10 metres long at the same time. How high is the building?

  • Facts and unknown:
    Tom’s height = 1.75 m   Building’s height (x) = ?
    Tom’s shadow = 1.09 m   Building’s shadow = 10m
  • Proportion:
 \frac{1.75m}{1.09m}=\frac{xm}{10m}
  • Cross multiply:
 (1.75)(10)=(1.09)(x)
  • Solve for x:
 x=\frac{(1.75)(10)}{1.09}=\frac{(\bcancel{1.09})x}{\bcancel{1.09}} Divide both sides by 1.09.
x=\frac{(1.75)(10)}{1.09}\approx16.055
The building’s height is 16.055m.
  • Check:
 \frac{1.75m}{1.09m}=\frac{16.055m}{10m} Replace x with 16.055.
(1.75) (10) = (16.055) (1.09)
17.5 = 17.5 Correct!

 

Example 1.4.3

If 15 mL of medicine must be mixed with 180 mL of water, how many mL of medicine must be mixed in 230 mL of water?

  • Proportion:
 \frac{15\;mL}{180\;mL}=\frac{x\;mL}{230\;mL} \frac{15\;mL\;medicine}{180\;mL\;water}=\frac{x\;mL\;medicine}{230\;mL\;water}
  • Cross multiply:
 (15)(230)=(180)(x)
  • Solve for x:
 x=\frac{(15\;mL)(230\;mL)}{180\;mL}\approx19.17\;mL
19.17 mL of medicine must be mixed in 230 mL of water.

 

Percent

Percent (%): one part per hundred.

Converting between percent, decimals and fractions:

Conversion Steps Example
Percent ⇒ Decimal Move the decimal point two places to the left, then remove %. 31%  =  31.% = 0.31
Decimal ⇒ Percent Move the decimal point two places to the right, then insert %. 0.317 = 0. 317 = 31.7 %
Percent ⇒ Fraction Remove %, divide by 100, then simplify.  15% = \frac{15}{100}=\frac{3}{20}
Fraction ⇒ Percent Divide, move the decimal point two places to the right, then insert %. \frac{1}{4} = 1÷4 = 0.25 = 25 %
Decimal ⇒ Fraction Convert the decimal to a percent, then convert the percent to a fraction. 0.35 = 35 % = \frac{35}{100}=\frac{7}{20}

% = per one hundred

 

There are two methods to solve percent problems:

  • Percent proportion method
  • Translation (translate the words into mathematical symbols.)

 

Percent proportion method:

\frac{Part}{Whole}=\frac{Percent}{100} or \frac{"is"\;number}{"of"\;number}=\frac{\%}{100}

 

Step Example
8 percent of what number is 4 ?
  • Identify the part, whole, and percent.
 ⇑

Percent

 ⇑

Whole (x)

 ⇑

Part
  • Set up the proportion equation.
 \frac{4}{x}=\frac{8}{100} \frac{Part}{Whole}=\frac{\%}{100}
  • Solve for unknown (x).
 x=\frac{(4)(100)}{8}=50 x=50

Translation method: translate the words into mathematical symbols.

  • What ____  x :    the word “what” represents an unknown quantity x.
  • Is      ____  = :    the word “is” represents an equal sign.
  • of     ____  × :    the word “of” represents a multiplication sign.
  • %    to     decimal:    always change the percent to a decimal.

 

Example 1.4.4

1)   What  is  15%  of  80?

                       x  =  0.15 • 80                         x = (0.15)(80) = 12  

 2)   What  percent  of  90  is  45?

                      x • 90 = 45                          x = \frac{45}{90} = 0.5 = 50%                       

 Divide both sides by 90.

 3)   12  is  8%  of  what number?

                      12 = 0.08 • x                           x = \frac{12}{0.08} = 150                               

Divide both sides by 0.08.

 

Percent increase or decrease:

Application Formula
Percent increase Percent increase = \frac{New\;value-Original\;value}{Original\;value} x=\frac{N-O}{O}
Percent decrease Percent decrease = \frac{Original\;value-New\;value}{Original\;value} x=\frac{O-N}{O}

 

Example 1.4.5

A product increased production from 1500 last month to 1650 this month.  Find the percent increase.

New value (N): 1650 This month.
Original value (O): 1500 Last month.
Percent increase: x=\frac{N-O}{O}=\frac{1650-1500}{1500}=0.1=10\%} A 10% increase.

 

A product was reduced from \bf{\$}33 to \bf{\$}29.  What percent reduction is this?

Percent decrease: x=\frac{O-N}{O}=\frac{33-29}{33}\approx0.12=12\% A 12 % decrease.

 

Practice questions

1. Write the following as a ratio or rate in lowest terms:

a. 4 nickels to 16 nickels.

b. 350 people for 1500 tickets.

c. 160 kilometres per 740 minutes.

2. A train travelled 459 km in 6 hours. What is the unit rate?

3. Write the following sentence as a proportion: 24 hours is to 1,940 kilometres as 12 hours is to 985 kilometres.   

4. 4 litres of juice cost $7.38, how much do 2 litres cost?

5. Sarah earns $4,500 in 30 days. How much does she earn in 120 days?

6. A product increased production from 2,800 last year to 3,920 this year. Find the percent increase.

7. The table below gives survey data regarding Ryerson Occupational and Public Health students and summer jobs, but some data are missing:

Year 2015 2016 2017
Unemployed students 350 ? 396
Total number of students 1250 1100 ?

a. What % of students were unemployed in 2015?

b. If the % of unemployed students remained the same in 2016, find the number of unemployed students in 2016.

c. If the % of unemployed students increased by an additional 5% in 2017, find the total number of students in 2017.

 

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Mathematics for Public and Occupational Health Professionals Copyright © 2019 by Ian Young is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.