7.1. Binomial Probability
Binomial Probability
In this section, we will consider types of problems that involve a sequence of trials, where each trial has only two outcomes, a success or a failure. These trials are independent. That is, the outcome of one does not affect the outcome of any other trial. Furthermore, the probability of success, p, and the probability of failure, (1 − p), remains the same throughout the experiment. These problems are called binomial probability problems. Since these problems were researched by a Swiss mathematician named Jacques Bernoulli around 1700, they are also referred to as Bernoulli trials.
We give the following definition:
Binomial Experiment: A binomial experiment satisfies the following four conditions:
- There are only two outcomes, a success or a failure, for each trial.
- The same experiment is repeated several times.
- The trials are independent; that is, the outcome of a particular trial does not affect the outcome of any other trial.
- The probability of success remains the same for every trial.
The probability model that we are about to investigate will give us the tools to solve many real-life problems like the ones given below.
- If a coin is flipped 10 times, what is the probability that it will fall heads 3 times?
- If a basketball player makes 3 out of every 4 free throws, what is the probability that he will make 7 out of 10 free throws in a game?
- If a medicine cures 80% of the people who take it, what is the probability that among the 10 people who take the medicine, 6 will be cured?
- If a microchip manufacturer claims that only 4% of their chips are defective, what is the probability that among the 60 chips chosen, exactly three are defective?
- If a telemarketing executive has determined that 15% of the people contacted will purchase the product, what is the probability that among the 12 people who are contacted, 2 will buy the product?
We now consider the following example to develop a formula for finding the probability of k successes in n Bernoulli trials.
Example 7.1.1
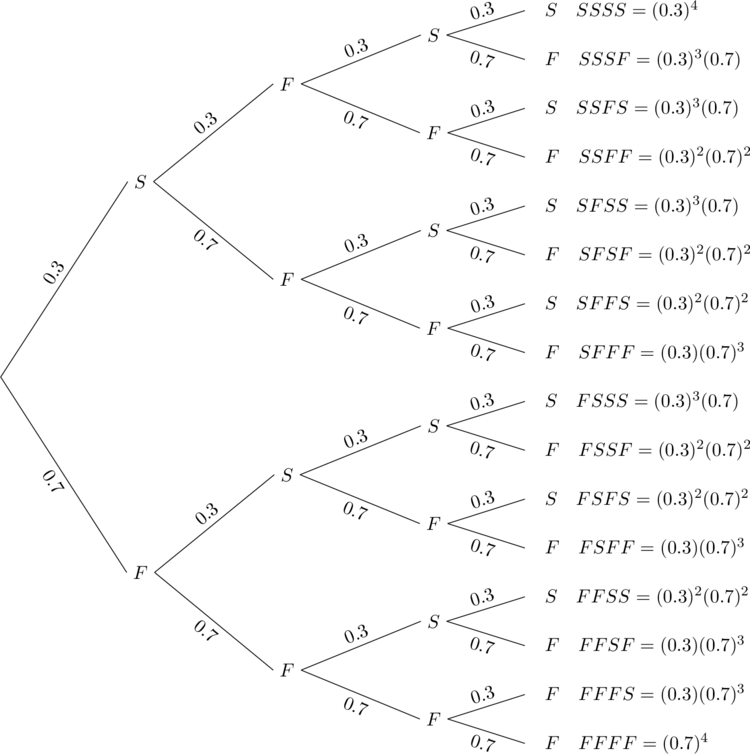
| Outcome | Four Hits | Three hits | Two Hits | One hits | No Hits |
| Probability | (0.3)4 | 4(0.3)3(0.7) | 6(0.3)2(0.7)2 | 4(0.3)(0.7)3 | (0.7)4 |
This gives us the following theorem:
Binomial Probability Theorem:
The probability of obtaining k successes in n independent Bernoulli trials is given by:
P(n, k; p) = nCkpkqn – k
where p denotes the probability of success and q = (1 − p) the probability of failure.
We use the above formula to solve the following examples.
Example 7.1.2
Example 7.1.3
Example 7.1.4
Example 7.1.5
Example 7.1.6
Practice questions
1. What is the probability of getting three ones if a die is rolled five times?
2. A basketball player has an 80% chance of sinking a basket on a free throw. In five free throws, what is the probability that he will sink:
a. Only one basket?
a. Three baskets?
c. At least three baskets?
3. If a medicine cures 75% of the people who take it, what is the probability that of 30 people who take the medicine:
a. 25 will be cured?
b. 26 will be cured?
c. 27 will be cured?
d. At least 25 will be cured?
4. The Canadian Food Inspection Agency (CFIA) has found that 5% of the imported spices into Canada are contaminated with pathogenic food-borne bacteria. What is the probability that a batch of 25 imported spices will have:
a. One contaminated product?
b. Two contaminated products?
5. An executive has determined that for a door-to-door donation initiative, 20% of the households visited will provide a donation. If 10 households are visited, what is the probability that at most 2 will provide a donation?

