7.4. Markov Chains
Markov Chains
We will now study stochastic processes, experiments in which the outcomes of events depend on the previous outcomes. Such a process or experiment is called a Markov Chain or Markov process. The process was first studied by a Russian mathematician named Andrei A. Markov in the early 1900s.
A small town is served by two telephone companies, Mama Bell and Papa Bell. Due to their aggressive sales tactics, each month 40% of Mama Bell customers switch to Papa Bell, that is, the other 60% stay with Mama Bell. On the other hand, 30% of the Papa Bell customers switch to Mama Bell. The above information can be expressed in a matrix which lists the probabilities of going from one state into another state. This matrix is called a transition matrix.
![Rendered by QuickLaTeX.com \begin{equation*} \mathbf{First\; Month\quad\quad} \begin{blockarray}{*{3}{c} l} \begin{block}{*{3}{>{$\footnotesize}c<{$}} l} & \BAmulticolumn{3}{c}{\textbf{Next Month}} & \\ & Mama Bell & Papa Bell \\ \end{block} \begin{block}{>{$\footnotesize}l<{$}[*{3}{c}]} Mama Bell & 0.60 & 0.40 \\ Papa Bell & 0.30 & 0.70 \\ \end{block} \end{blockarray} \end{equation*}](https://pressbooks.library.torontomu.ca/ohsmath/wp-content/ql-cache/quicklatex.com-ad12220e5c58c845019277314d4a0319_l3.png)
The reader should observe that a transition matrix is always a square matrix because all possible states must have both rows and columns. All entries in a transition matrix are non-negative as they represent probabilities. Furthermore, since all possible outcomes are considered in the Markov process, the sum of the row entries is always 1.
Example 7.4.1
![Rendered by QuickLaTeX.com \begin{equation*} \mathbf{First\; Day\quad\quad} \begin{blockarray}{*{3}{c} l} \begin{block}{*{3}{>{$\footnotesize}c<{$}} l} & \BAmulticolumn{3}{c}{\textbf{Next Day}} & \\ & Walk & Bicycle \\ \end{block} \begin{block}{>{$\footnotesize}l<{$}[*{3}{c}]} Walk & 1/2 & 1/2 \\ Bicycle & 1/4 & 3/4 \\ \end{block} \end{blockarray} \end{equation*}](https://pressbooks.library.torontomu.ca/ohsmath/wp-content/ql-cache/quicklatex.com-3ad0d6fcd7e9146ec321e7870bd53d2c_l3.png)
Example 7.4.2
Let W denote that Professor Symons walks and B denote that he rides his bicycle. We use the following tree diagram to compute the probabilities.
| Monday | Tuesday | Wednesday |
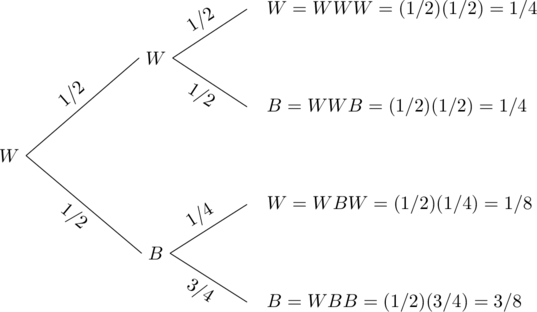
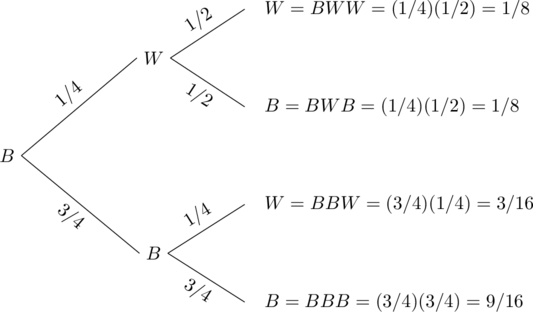
The probability that Professor Symons walked on Wednesday given that he walked on Monday can be found from the tree diagram, as listed below.
P(Walked Wednesday | Walked Monday) = P(WWW) + P(WBW) = 1/4 + 1/8 = 3/8.
P(Bicycled Wednesday | Walked Monday) = P(WWB) + P(WBB) = 1/4 + 3/8 = 5/8.
P(Walked Wednesday | Bicycled Monday) = P(BWW) + P(BBW) = 1/8 + 3/16 = 5/16.
P(Bicycled Wednesday | Bicycled Monday) = P(BWB) + P(BBB) = 1/8 + 9/16 = 11/16.
We represent the results in the following matrix:
![Rendered by QuickLaTeX.com \begin{equation*} \mathbf{Monday\quad\quad} \begin{blockarray}{*{3}{c} l} \begin{block}{*{3}{>{$\footnotesize}c<{$}} l} & \BAmulticolumn{3}{c}{\textbf{Wednesday}} & \\ & Walk & Bicycle \\ \end{block} \begin{block}{>{$\footnotesize}l<{$}[*{3}{c}]} Walk & 3/8 & 5/8 \\ Bicycle & 5/16 & 11/16 \\ \end{block} \end{blockarray} \end{equation*}](https://pressbooks.library.torontomu.ca/ohsmath/wp-content/ql-cache/quicklatex.com-898aeb9a34a09a972a4e35fb1202a913_l3.png)
Alternately, this result can be obtained by squaring the original transition matrix.
We list both the original transition matrix T and T2 as follows:
![]()
![]()
![]()
![]()
![]()
The reader should compare this result with the probabilities obtained from the tree diagram. Consider the following case, for example:
P(Walked Wednesday | Bicycled Monday) = P(BWW) + P(BBW) = 1/8 + 3/16 = 5/16.
It makes sense because to find the probability that Professor Symons will walk on Wednesday given that he bicycled on Monday, we sum the probabilities of all paths that begin with B and end in W. There are two such paths, and they are BWW and BBW.
Certain Markov chains, called regular Markov chains, tend to stabilize in the long run. It so happens that the transition matrix we have used in the the above examples is just such a Markov chain. The next example deals with the long term trend or steady-state situation for that matrix.
Example 7.4.3
When this happens, we say that the system is in steady-state or state of equilibrium. In this situation, all row vectors are equal. If the original matrix is an n by n matrix, we get n vectors that are all the same. We call this vector a fixed probability vector or the equilibrium vector E. In the above problem, the fixed probability vector E is ![]() . Furthermore, if the equilibrium vector E is multiplied by the original matrix T, the result is the equilibrium vector E. That is,
. Furthermore, if the equilibrium vector E is multiplied by the original matrix T, the result is the equilibrium vector E. That is,
ET = E
or,
![]()
Regular Markov Chains
A Markov chain reaches a state of equilibrium if it is a regular Markov chain. A Markov chain is said to be a regular Markov chain if some power of it has only positive entries.
As we take higher powers of T, Tn, as n becomes large, approaches a state of equilibrium. The equilibrium distribution vector E can be found by letting ET = E.
Example 7.4.4
![Rendered by QuickLaTeX.com \begin{equation*} \mathbf{First\; Month\quad\quad} \begin{blockarray}{*{3}{c} l} \begin{block}{*{3}{>{$\footnotesize}c<{$}} l} & \BAmulticolumn{3}{c}{\textbf{Next Month}} & \\ & Mama Bell & Papa Bell \\ \end{block} \begin{block}{>{$\footnotesize}l<{$}[*{3}{c}]} Mama Bell & 0.60 & 0.40 \\ Papa Bell & 0.30 & 0.70 \\ \end{block} \end{blockarray} \end{equation*}](https://pressbooks.library.torontomu.ca/ohsmath/wp-content/ql-cache/quicklatex.com-ad12220e5c58c845019277314d4a0319_l3.png)
If the initial market share for Mama Bell is 20% and for Papa Bell 80%, we’d like to know the long term market share for each company.
Let matrix T denote the transition matrix for this Markov chain, and M denote the matrix that represents the initial market share. Then T and M are as follows:
![]() and
and ![]()
Since each month the town’s people switch according to the transition matrix T, after one month the distribution for each company is as follows:
![Rendered by QuickLaTeX.com \left[\begin{array}{cc} 0.20 & 0.80\end{array}\right] \left[\begin{array}{cc} 0.60 & 0.40 \\0.30 & 0.70\end{array}\right]=\left[\begin{array}{cc} (0.20)(0.60) + (0.80)(0.30) & (0.20)(0.40) + (0.80)(0.70)\end{array}\right]=\left[\begin{array}{cc} 0.36 & 0.64\end{array}\right]](https://pressbooks.library.torontomu.ca/ohsmath/wp-content/ql-cache/quicklatex.com-9852c71ab1388c813e80aef3970dfb55_l3.png)
After two months, the market share for each company is:
![]()
After three months the distribution is:
![]()
After four months the market share is:
![]()
After 30 months the market share is ![]() .
.
The market share after 30 months has stabilized to ![]() .
.
This means that:
![]()
Once the market share reaches an equilibrium state, it stays the same, that is, ET = E.
Can the equilibrium vector E be found without raising the transition matrix to large powers? The answer to this question provides us with a way to find the equilibrium vector E. The answer lies in the fact that ET = E. Since we have the matrix T, we can determine E from the statement ET = E. The example below illustrates this approach.
Example 7.4.5
Practice questions
1. A survey of American car buyers indicates that if a person buys a Ford, there is a 60% chance that their next purchase will be a Ford, while owners of a GM will buy a GM again with a probability of 0.80. Express the buying habits of these consumers in a transition matrix.
2. A hockey player decides to either shoot the puck (S) or pass it to a teammate (P) according to the following transition matrix.
![Rendered by QuickLaTeX.com \begin{equation*} \mathbf{Previous\; Play\quad\quad} \begin{blockarray}{*{3}{c} l} \begin{block}{*{3}{>{$\footnotesize}c<{$}} l} & \BAmulticolumn{3}{c}{\textbf{Next Play}} & \\ & \quad\quad S\quad\quad & \quad\quad P\quad\quad \\ \end{block} \begin{block}{>{$\footnotesize}l<{$}[*{3}{c}]} Shoot (S) & \quad 0.60 & \quad 0.40 \\ Pass (P) & \quad 0.80 & \quad 0.20 \\ \end{block} \end{blockarray} \end{equation*}](https://pressbooks.library.torontomu.ca/ohsmath/wp-content/ql-cache/quicklatex.com-0664fe22034565b606c615b9e2f47cce_l3.png)
Find the following:
a. If the player shot on the first play, what is the probability that he will pass on the third play?
b. What is the long-term shoot vs. pass distribution of this player?
3. The local police department conducts a campaign to reduce the rates of texting and driving in the community. The effects of the campaign are summarized in the transition matrix below:
![Rendered by QuickLaTeX.com \begin{equation*} \mathbf{Before\quad\quad} \begin{blockarray}{*{3}{c} l} \begin{block}{*{3}{>{$\footnotesize}c<{$}} l} & \BAmulticolumn{3}{c}{\textbf{After}} & \\ & \quad\quad Y\quad\quad & \quad\quad N\quad\quad \\ \end{block} \begin{block}{>{$\footnotesize}l<{$}[*{3}{c}]} Texts and Drives (Y) & \quad 0.70 & \quad 0.30 \\ Doesn't Text and Drive (N) & \quad 0.10 & \quad 0.90 \\ \end{block} \end{blockarray} \end{equation*}](https://pressbooks.library.torontomu.ca/ohsmath/wp-content/ql-cache/quicklatex.com-c9478ad599bc1de994375ab87d742639_l3.png)
If 35% of people in the community reported texting and driving before the campaign:
a. What is the percentage of people in the community that reported texting and driving after the campaign?
b. If the campaign were to be repeated multiple times, what is the long-range trend in terms of the lowest rate that texting and driving can be reduced to in this community?
4. A large company conducted a training program with their employees to reduce the incidence of slips, trips and falls in the workplace. About 15% of workers reported a slip, trip or fall accident the previous year (year 1). After the training program (year 2), 75% of those who previously reported an accident reported no further accidents, while 5% of those who didn’t report a previous accident reported one this year.
a. Create a transition matrix for this scenario.
b. If the company employs 8500 workers, how many slip, trip and fall accidents were reported in year 2?
c. If the program continued for another year, how many accidents would be reported in year 3?
d. If the training program were to be repeated for many years, what is the lowest prevalence of slip, trip or fall accidents that could be achieved?

