2.1. Graphing a Linear Equation
Graphing a Linear Equation
Equations whose graphs are straight lines are called linear equations. The following are some examples of linear equations:
A line is completely determined by two points. Therefore, to graph a linear equation, we need to find the coordinates of two points. This can be accomplished by choosing an arbitrary value for x or y and then solving for the other variable.
Example 2.1.1
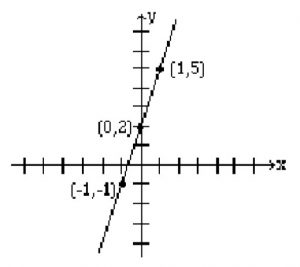
Graph the line: y = 3x + 2
Solution
We need to find the coordinates of at least two points.
We arbitrarily choose x = -1 , x = 0 , and x = 1.
If x = -1, then y = 3(-1) + 2 or -1. Therefore, (-1, -1) is a point on this line.
If x = 0, then y = 3(0) + 2 or y = 2. Hence the point (0, 2).
If x = 1, then y = 5, and we get the point (1, 5). Below, the results are summarized, and the line is graphed.
| X | -1 | 0 | 1 |
| Y | -1 | 2 | 5 |
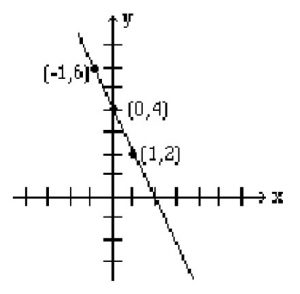
Example 2.1.2
If y = 2, then 2x + 2 = 4, which yields x = 1, and gives the point (1, 2). The table below shows the points, and the line is graphed.
| x | -1 | 0 | 1 |
| y | 6 | 4 | 2 |
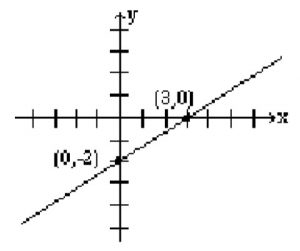
The points at which a line crosses the coordinate axes are called the intercepts. When graphing a line, intercepts are preferred because they are easy to find. In order to find the x-intercept, we let y = 0, and to find the y-intercept, we let x = 0.
Example 2.1.3
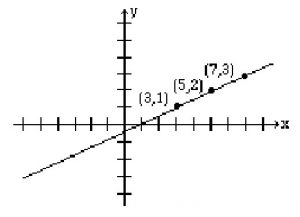
Example 2.1.4
The results are given in the table below.
| t | 0 | 1 | 2 |
| x | 3 | 5 | 7 |
| y | 1 | 2 | 3 |
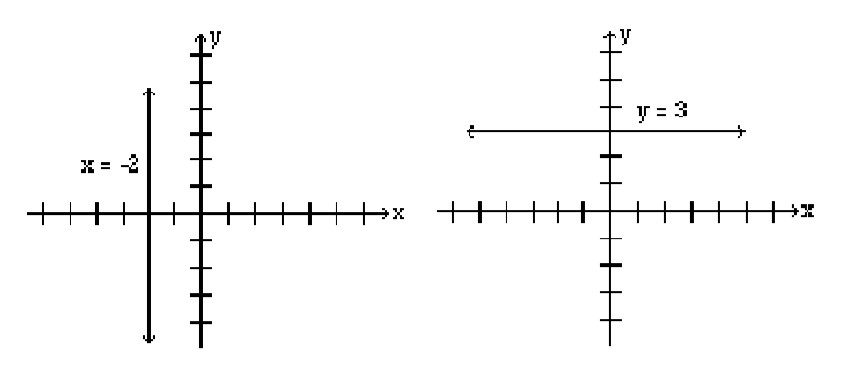
Horizontal and Vertical Lines
When an equation of a line has only one variable, the resulting graph is a horizontal or a vertical line.
The graph of the line x = a, where a is a constant, is a vertical line that passes through the point ( a, 0). Every point on this line has the x-coordinate a, regardless of the y-coordinate.
The graph of the line y = b, where b is a constant, is a horizontal line that passes through the point (0, b). Every point on this line has the y-coordinate b, regardless of the x-coordinate.
Example 2.1.5
Note: Most students feel that the coordinates of points must always be integers. This is not true, and in real life situations, not always possible. Do not be intimidated if your points include numbers that are fractions or decimals.
Practice questions
1. Is the point (2, 3) on the line 5x – 2y = 4?
2. For the line 3x – y = 12, complete the following ordered pairs:
a. (2, ?) (? , 6)
b. (0, ?) (?, 0)
3. Graph y = 4x – 3
4. Graph 2x + 4 = 0
5. Graph the line using the parametric equations: x = 1 + 2t; y = 3 + t.
6. Graph the following three equations on the same set of coordinate axes: y = x + 1; y = 2x + 1; y = –x + 1.

