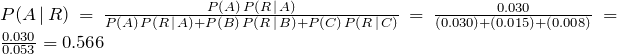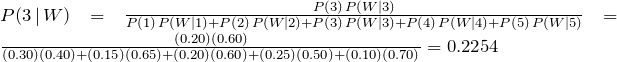Bayes’ Formula
In this section, we will develop and use Bayes’ Formula to solve an important type of probability problem. Bayes’ formula is a method of calculating the conditional probability P(F | E) from P(E | F). The ideas involved here are not new, and most of these problems can be solved using a tree diagram. However, Bayes’ formula does provide us with a tool with which we can solve these problems without a tree diagram. We begin with an example.
Suppose you are given two jars. Jar I contains one black and 4 white marbles, and Jar II contains 4 black and 6 white marbles. If a jar is selected at random and a marble is chosen:
a. What is the probability that the marble chosen is a black marble?
b. If the chosen marble is black, what is the probability that it came from Jar I?
c. If the chosen marble is black, what is the probability that it came from Jar II?
Solution
Let JI be the event that Jar I is chosen, JII be the event that Jar II is chosen, B be the event that a black marble is chosen and W the event that a white marble is chosen. We illustrate using a tree diagram.
|

(a)
|
(b)
|
a. The probability that a black marble is chosen is P(B) = 1/10 + 2/10 = 3/10.
b. To find P(JI | B), we use the definition of conditional probability, and we get
c. Similarly,
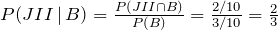
In parts b and c, the reader should note that the denominator is the sum of all probabilities of all branches of the tree that produce a black marble, while the numerator is the branch that is associated with the particular jar in question.
This is a statement of Bayes’ formula.
Bayes’ Formula:Let S be a sample space that is divided into n partitions, A1, A2, . . . An. If E is any event in S, then:
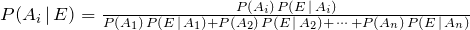
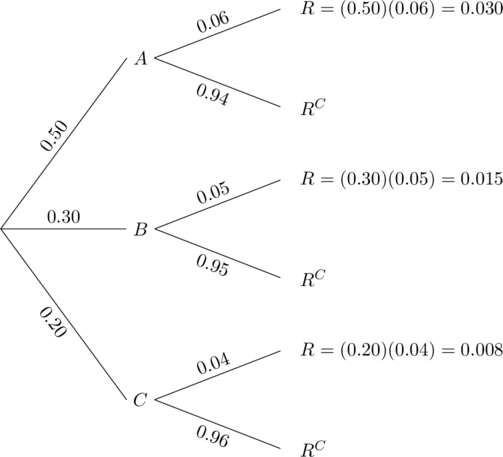
A department store buys 50% of its appliances from Manufacturer A, 30% from Manufacturer B, and 20% from Manufacturer C. It is estimated that 6% of Manufacturer A’s appliances, 5% of Manufacturer B’s appliances, and 4% of Manufacturer C’s appliances need repair before the warranty expires. An appliance is chosen at random. If the appliance chosen needed repair before the warranty expired, what is the probability that the appliance was manufactured by Manufacturer A? Manufacturer B? Manufacturer C?
Solution
Let events A, B and C be the events that the appliance is manufactured by Manufacturer A, Manufacturer B, and Manufacturer C, respectively. Further, suppose that the event R denotes that the appliance needs repair before the warranty expires.
We need to find P(A | R), P(B | R) and P(C | R).
We will do this problem both by using a tree diagram and by using Bayes’ formula.
We draw a tree diagram.
The probability P(A | R), for example, is a fraction whose denominator is the sum of all probabilities of all branches of the tree that result in an appliance that needs repair before the warranty expires, and the numerator is the branch that is associated with Manufacturer A. P(B | R) and P(C | R) are found in the same way. We list both as follows:
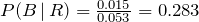
and
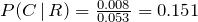
.
Alternatively, using Bayes’ formula:
P(B | R) and P(C | R) can be determined in the same manner.
There are five Jacy’s department stores in San Jose. The distribution of number of employees by gender is given in the table below.
| Store Number |
Number of Employees |
Proportion of Women Employees |
| 1 |
300 |
0.40 |
| 2 |
150 |
0.65 |
| 3 |
200 |
0.60 |
| 4 |
250 |
0.50 |
| 5 |
100 |
0.70 |
|
Total = 1000 |
|
If an employee chosen at random is a woman, what is the probability that the employee works at store III?
Solution
Let k = 1, 2, …, 5 be the event that the employee worked at store k, and W be the event that the employee is a woman. Since there are a total of 1000 employees at the five stores,
P(1) = 0.30 P(2) = 0.15 P(3) = 0.20 P(4) = 0.25 P(5) = 0.10
Using Bayes’ formula,
For certain problems, we can use a much more intuitive approach than Bayes’ Formula.
A certain disease has an incidence rate of 2%. A test is available to test for the disease, but it is not perfect. The
false negative rate is 10% (that is, about 10% of people who take the test will test negative, even though they actually have the disease). The
false positive rate is 1% (that is, about 1% of people who take the test will test positive, even though they do not actually have the disease). Compute the probability that a person who tests positive actually has the disease:
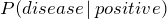
Imagine 10,000 people are tested. Of these 10,000, 200 will have the disease; 10% of them, or 20, will test negative and the remaining 180 will test positive. Of the 9800 who do not have the disease, 1% of them, or 98, will test positive. These data can be summarized in a table as follows:
|
Positive test |
Negative test |
Total |
| Have disease |
180 |
20 |
200 |
| Do not have disease |
98 |
9,702 |
9,800 |
| Total |
278 |
9,822 |
10,000 |
Solution
So of the 278 people who test positive, 180 will have the disease. Thus:
So about 65% of the people who test positive will have the disease.
Using Bayes’ formula directly would give the same result:
Practice questions
1. Jar I contains five red and three white marbles, and Jar II contains four red and two white marbles. A jar is picked at random and a marble is drawn. Draw a tree diagram and find the following probabilities:
a. P (Marble is red)
b. P (The marble came from Jar II given that a white marble is drawn)
c. P (Red marble | Jar I)
2. The table below summarizes the results of a diagnostic test:
|
Positive test |
Negative test |
Total |
| Have disease |
105 |
15 |
120 |
| Do not have disease |
40 |
640 |
680 |
| Total |
145 |
655 |
800 |
Using the table, compute the following:
a. P (Negative test | disease positive)
b. P (Disease positive | test positive)
3. A computer company buys its chips from three different manufacturers. Manufacturer I provides 60% of the chips, of which 5% are known to be defective; Manufacturer II supplies 30% of the chips, of which 4% are defective; while the rest are supplied by Manufacturer III, of which 3% are defective. If a chip is chosen at random, find the following probabilities:
a. P (The chip is defective)
b. P (The chip came from Manufacturer II | it is defective)
c. P (The chip is defective | it came from manufacturer III)
4. The following table shows the percent of “Conditional Passes” that different types of food premises received in a city during their last public health inspection.
| Premise Type |
Number of Premises |
Proportion that Received Conditional Pass |
| Restaurant |
2000 |
0.07 |
| Grocery Store |
425 |
0.03 |
| Cafe/Bar |
1865 |
0.05 |
| Food Truck/Cart |
150 |
0.08 |
| Other |
560 |
0.05 |
|
Total = 5000 |
|
If a premise is selected at random, find the following probabilities:
a. P (Received Conditional Pass)
b. P (Received Conditional Pass | Restaurant)
c. P (Grocery Store | Received Conditional Pass)
![]()