6.3. Probability Using Tree Diagrams and Combinations
Probability Using Tree Diagrams and Combinations
In this section, we will apply previously learnt counting techniques in calculating probabilities, and use tree diagrams to help us gain a better understanding of what is involved.
We begin with an example.
Suppose a jar contains 3 red and 4 white marbles. If two marbles are drawn with replacement, what is the probability that both marbles are red?
Solution
Let E be the event that the first marble drawn is red, and let F be the event that the second marble drawn is red.
We need to find
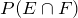
.
By the statement, “two marbles are drawn with replacement,” we mean that the first marble is replaced before the second marble is drawn.
There are 7 choices for the first draw. And since the first marble is replaced before the second is drawn, there are, again, seven choices for the second draw. Using the multiplication axiom, we conclude that the sample space S consists of 49 ordered pairs. Of the 49 ordered pairs, there are 3 × 3 = 9 ordered pairs that show red on the first draw and, also, red on the second draw. Therefore:
Further note that in this particular case:
If in the previous example, the two marbles are drawn without replacement, then what is the probability that both marbles are red?
Solution
By the statement, “two marbles are drawn without replacement,” we mean that the first marble is not replaced before the second marble is drawn.
Again, we need to find
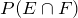
.
There are, again, 7 choices for the first draw. And since the first marble is not replaced before the second is drawn, there are only six choices for the second draw. Using the multiplication axiom, we conclude that the sample space S consists of 42 ordered pairs. Of the 42 ordered pairs, there are 3 × 2 = 6 ordered pairs that show red on the first draw and red on the second draw. Therefore,
Here 3/7 represents
P(
E), and 2/6 represents the probability of drawing a red on the second draw, given that the first draw resulted in a red. We write the latter as
P(Red on the second | red on first) or
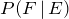
. The “|” represents the word “given.” Therefore:
The above result is an important one and will appear again in later sections.
We now demonstrate the above results with a tree diagram.
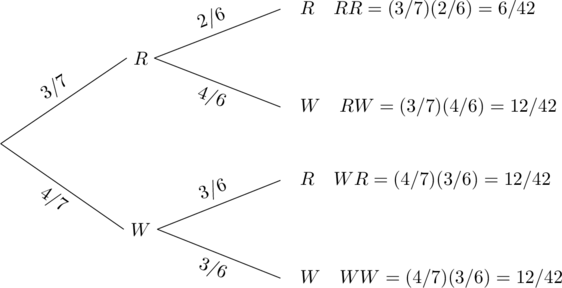
Suppose a jar contains 3 red and 4 white marbles. If two marbles are drawn without replacement, find the following probabilities using a tree diagram.
a. The probability that both marbles are white.
b. The probability that the first marble is red and the second white.
c. The probability that one marble is red and the other white.
Solution
Let R be the event that the marble drawn is red, and let W be the event that the marble drawn is white. We draw the following tree diagram:
Although the tree diagrams give us better insight into a problem, they are not practical for problems where more than two or three things are chosen. In such cases, we use the concept of combinations that we learned in Chapter 5. This method is best suited for problems where the order in which the objects are chosen is not important, and the objects are chosen without replacement.
Suppose a jar contains 3 red, 2 white, and 3 blue marbles. If three marbles are drawn without replacement, find the following probabilities:
a. P(Two red and one white)
b. P(One of each color)
c. P(None blue)
d. P(At least one blue)
Solution
Let us suppose the marbles are labeled as R1, R2, R3, W1, W2, B1, B2, B3.
a. P(Two red and one white)
We analyze the problem in the following manner.
Since we are choosing 3 marbles from a total of 8, there are 8C3 = 56 possible combinations. Of these 56 combinations, there are 3C2 × 2C1 = 6 combinations consisting of 2 red and one white. Therefore:
P(Two red and one white) =
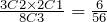
.
b. P(One of each color)
Again, there are 8C3 = 56 possible combinations. Of these 56 combinations, there are 3C1 × 2C1 × 3C1 = 18 combinations consisting of one red, one white, and one blue. Therefore:
P(One of each color) =
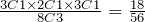
.
c. P(None blue)
There are 5 non-blue marbles, therefore:
P(None blue) =
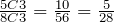
.
d. P(At least one blue)
By “at least one blue marble,” we mean the following: one blue marble and two non-blue marbles, or two blue marbles and one non-blue marble, or all three blue marbles. So we have to find the sum of the probabilities of all three cases.
P(At least one blue) = P(one blue, two non-blue) + P(two blue, one non-blue) + P(three blue)
P(At least one blue) =

P(At least one blue) = 30/56 + 15/56 + 1/56 = 46/56 = 23/28.
Alternately, we use the fact that P(E) = 1 − P(Ec).
If the event E = At least one blue, then Ec = None blue. But from part c of this example, we have (Ec) = 5/28. Therefore:
P(E) = 1 − 5/28 = 23/28.
Five cards are drawn from a deck. Find the probability of obtaining two pairs, that is, two cards of one value, two of another value, and one other card.
Solution
Let us first do an easier problem–the probability of obtaining a pair of kings and queens.
Since there are four kings, and four queens in the deck, the probability of obtaining two kings, two queens and one other card is:
P(A pair of kings and queens) =
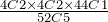
To find the probability of obtaining two pairs, we have to consider all possible pairs. Since there are altogether 13 values, that is, aces, deuces, and so on, there are 13C2 different combinations of pairs.
P(Two pairs) =
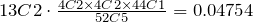
We end the section by solving a problem called the Birthday Problem.
If there are 25 people in a room, what is the probability that at least two people have the same birthday?
Solution
Let event E represent that at least two people have the same birthday. We first find the probability that no two people have the same birthday. We analyze as follows.
Suppose there are 365 days to every year. According to the multiplication axiom, there are 36525 possible birthdays for 25 people. Therefore, the sample space has 36525 elements. We are interested in the probability that no two people have the same birthday. There are 365 possible choices for the first person and since the second person must have a different birthday, there are 364 choices for the second, 363 for the third, and so on. Therefore:
P(No two have the same birthday) =
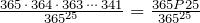
Since P(at least two people have the same birthday) = 1 − P (No two have the same birthday):
P(at least two people have the same birthday) =
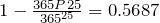
Practice questions
1. Two apples are chosen from a basket containing five red and three yellow apples. Draw a tree diagram and find the following probabilities:
a. P (both red)
b. P (both yellow)
2. Three marbles are drawn from a jar containing five red, four white, and three blue marbles. Find the following probabilities using combinations:
a. P (all three red)
b. P (none white)
3. A committee of four is selected from a total of 4 occupational and public health students, 5 nursing students, and 6 nutrition students. Find the probabilities for the following events:
a. At least three occupational and public health students are selected.
b. All four students of the same program are selected.
c. Exactly three students of the same program are selected.
4. A hockey team has 2 goalies, 6 defense players, 8 wingers, and 4 centers. If the team randomly selects 5 players to attend a charity function, what is the probability that:
a. They are all wingers?
b. No goalies or centers are selected?
c. Two defensive players and one player from each other position are selected?
d. At least one goalie is selected?
5. Complete the following birthday problems:
a. If there are 10 people in a room, what is the probability that no two have the same birthday?
b. If there are 35 people in a room, what is the probability that at least two have the same birthday?