6.2. Mutually Exclusive Events and the Addition Rule
Mutually Exclusive Events and the Addition Rule
In the previous chapter, we learned to find the union, intersection, and complement of a set. We will now use these set operations to describe events.
The union of two events E and F, 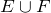 , is the set of outcomes that are in E or in F or in both.
, is the set of outcomes that are in E or in F or in both.
The intersection of two events E and F,  , is the set of outcomes that are in both E and F.
, is the set of outcomes that are in both E and F.
The complement of an event E, denoted by Ec, is the set of outcomes in the sample space S that are not in E. It is worth noting that P(Ec) = 1 − P (E). This follows from the fact that if the sample space has n elements and E has k elements, then Ec has n − k elements. Therefore:
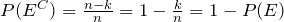
Of particular interest to us are the events whose outcomes do not overlap. We call these events mutually exclusive.
Two events E and F are said to be mutually exclusive if they do not intersect. That is,  =∅.
=∅.
Next we’ll determine whether a given pair of events are mutually exclusive.
A card is drawn from a standard deck. Determine whether the pair of events given below is mutually exclusive.
E = {The card drawn is an Ace}
F = {The card drawn is a heart}
Solution
Clearly the ace of hearts belongs to both sets. That is:

= {Ace of hearts} ≠ ∅.
Therefore, the events E and F are not mutually exclusive.
Two dice are rolled. Determine whether the pair of events given below is mutually exclusive.
G = {The sum of the faces is six}
H = {One die shows a four}
Solution
For clarity, we list the elements of both sets:
G = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
H = {(2, 4), (4, 2)}
Clearly,

= {(2, 4), (4, 2)} ≠ Ø.
Therefore, the two sets are not mutually exclusive.
A family has three children. Determine whether the following pair of events are mutually exclusive.
M ={The family has at least one boy}
N ={The family has all girls}
Solution
Although the answer may be clear, we list both the sets:
M ={BBB , BBG , BGB , BGG , GBB , GBG , GGB} and N ={GGG}
Clearly,

= Ø
Therefore, the events M and N are mutually exclusive.
We will now consider problems that involve the union of two events.
If a die is rolled, what is the probability of obtaining an even number or a number greater than four?
Solution
Let E be the event that the number shown on the die is an even number, and let F be the event that the number shown is greater than four.
The sample space S ={1, 2, 3, 4, 5, 6}. The event E ={2, 4, 6}, and the event F ={5, 6}
We need to find
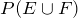
.
Since
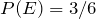
, and
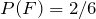
, a student may say
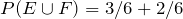
. This will be incorrect because the element 6, which is in both
E and
F has been counted twice, once as an element of
E and once as an element of
F. In other words, the set
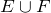
has only four elements and not five. Therefore,
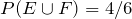
and not
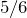
.
This can be illustrated by a Venn diagram. The sample space
S, the events
E and
F, and

are listed below.
S = {1, 2, 3, 4, 5, 6} , E = {2, 4, 6} , F = {5, 6} , and  = {6}.
= {6}.
The above figure shows
S,
E,
F, and

.
Finding the probability of
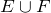
, is the same as finding the probability that
E will happen, or
F will happen, or both will happen. If we count the number of elements
n(
E) in
E, and add to it the number of elements
n(
F) in
F, the points in both
E and
F are counted twice, once as elements of
E and once as elements of
F. Now if we subtract from the sum,
n(
E) +
n(
F), the number
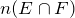
, we remove the duplicity and get the correct answer. So as a rule:
When expressed as a probability:
Applying the above for this example, we get:
This is because, when we add
P(
E) and
P(
F), we have added
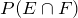
twice. Therefore, we must subtract
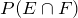
, once.
The above example gives us the general formula, called the Addition Rule, for finding the probability of the union of two events. It states:
If two events
E and
F are mutually exclusive, then
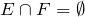
and
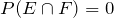
, and we get:
If a card is drawn from a deck, use the addition rule to find the probability of obtaining an ace or a heart.
Solution
Let A be the event that the card is an ace, and H the event that it is a heart. Since there are four aces, and 13 hearts in the deck, P(A) = 4/52 and P(H) = 13/52.
Furthermore, since the intersection of two events is an ace of hearts,
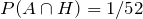
We need to find
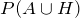
:
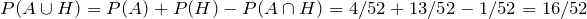
.
Two dice are rolled, and the events F and T are as follows:
F = {The sum of the dice is four} and T = {At least one die shows a three}
Find
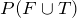
.
Solution
We list
F and
T, and

as follows:
F = {(1, 3), (2, 2), (3, 1)}
T = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1, 3), (2, 3), (4, 3), (5, 3), (6, 3)}

= {(1, 3), (3, 1)}
Since
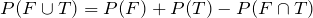
We have
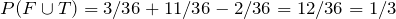
.
Mr. Washington is seeking a mathematics instructor’s position at a university. His employment depends on two conditions: whether the board approves the position, and whether the hiring committee selects him. There is a 80% chance that the board will approve the position, and there is a 70% chance that the hiring committee will select him. If there is a 90% chance that at least one of the two conditions, the board approval or his selection, will be met, what is the probability that Mr. Washington will be hired?
Solution
Let A be the event that the board approves the position, and S be the event that Mr. Washington gets selected. We have:
We need to find,
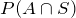
.
The addition formula states that:
Substituting the known values, we get:
Therefore,
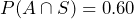
.
The probability that this weekend will be cold is 0.6, the probability that it will be rainy is 0.7, and probability that it will be both cold and rainy is 0.5. What is the probability that it will be neither cold nor rainy?
Solution
Let C be the event that the weekend will be cold, and R be event that it will be rainy. We are given that:
We want to find
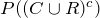
:
We summarize this section by listing the important rules.
- The Addition Rule: For two events E and F,
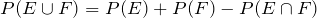
- The Addition Rule for Mutually Exclusive Events: If two events E and F are mutually exclusive, then
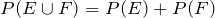
- The Complement Rule: If Ec is the complement of event E, then
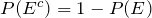
Practice questions
1. Determine whether the following pairs of events are mutually exclusive:
a. Three coins are tossed. A = {Two heads come up}, B = {At least one tail comes up}.
b. Two dice a rolled. C = {The sum of the dice is 9}, D = {At least one dice shows a 2}.
c. E = {You will get an A on your next exam}, F = {You will pass your next exam}.
2. Two dice are rolled, and the events G and H are as follows. G = {The sum of the dice is 8}, H = {Exactly one die shows a 6}. Use the addition rule to find 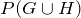 .
.
3. At Ryerson University, 20% of the students take a Mathematics course, 30% take a Statistics course, and 10% take both. What percentage of students take either a Mathematics or Statistics course?
4. The following table shows the distribution of coffee drinkers by gender:
| Coffee drinker |
Males (M) |
Females (F) |
TOTAL |
| Yes (Y) |
31 |
33 |
64 |
| No (N) |
19 |
17 |
36 |
|
50 |
50 |
100 |
Use the table to determine the following probabilities:
a. 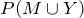
b. 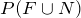
5. If 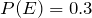 ,
, 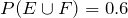 , and
, and 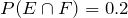 , use the addition rule to find
, use the addition rule to find 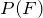 .
.
6. A provincial park has 240 campsites. A total of 90 sites have electricity. Of the 66 sites on the lakeshore, 24 of them have electricity. If a site is selected at random, what is the probability that:
a. It will have electricity?
b. It will have electricity or be on the lakeshore?
c. It will be on the lakeshore and not have electricity?
![]() , is the set of outcomes that are in E or in F or in both.
, is the set of outcomes that are in E or in F or in both.![]() , is the set of outcomes that are in both E and F.
, is the set of outcomes that are in both E and F.![]()
![]() =∅.
=∅.![]() = {6}.
= {6}.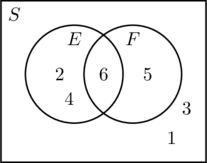
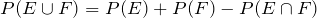
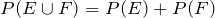
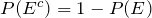
![]() .
.![]()
![]()
![]() ,
, ![]() , and
, and ![]() , use the addition rule to find
, use the addition rule to find ![]() .
.
