Combinations
Suppose we have a set of three letters {A,B,C}, and we are asked to make two-letter word sequences. We have the following six permutations:
AB BA BC CB AC CA
Now suppose we have a group of three people {A,B,C} as Al, Bob, and Chris, respectively, and we are asked to form committees of two people each. This time we have only three committees, namely:
AB BC AC
When forming committees, the order is not important, because the committee that has Al and Bob is no different than the committee that has Bob and Al. As a result, we have only three committees and not six. Forming word sequences is an example of permutations, while forming committees is an example of combinations – the topic of this section.
Permutations are those arrangements where order is important, while combinations are those arrangements where order is not significant. From now on, this is how we will tell permutations and combinations apart.
Just as the symbol nPr represents the number of permutations of n objects taken r at a time, nCr represents the number of combinations of n objects taken r at a time.
Our next goal is to determine the relationship between the number of combinations and the number of permutations in a given situation.
Given the set of letters {A,B,C,D}. Write the number of combinations of three letters, and then from these combinations determine the number of permutations.
Solution
We have the following four combinations:
ABC BCD CDA BDA
Since every combination has three letters, there are 3! permutations for every combination. We list them below:
ABC BCD CDA BDA
ACB BDC CAD BAD
BAC CDB DAC DAB
BCA CBD DCA DBA
CAB DCB ACD ADB
CBA DBC ADC ABD
The number of permutations are 3! times the number of combinations. That is:
4P3 = 3! · 4C3
or 4C3 =
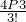
In general, nCr = 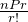
Since nPr = 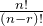
We have, nCr = 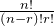
Summarizing:
- Combinations: A combination of a set of elements is an arrangement where each element is used once, and order is not important.
- The Number of Combinations of n Objects Taken r at a Time: nCr =
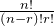 , where n and r are natural numbers.
, where n and r are natural numbers.
Compute:
a. 5C3
b. 7C3.
Solution
We use the above formula:
In how many different ways can a student answer five questions from a test that has seven questions, if the order of the selection is not important?
Solution
Since the order is not important, it is a combination problem, and the answer is:
7C5 = 21.
How many line segments can be drawn by connecting any two of the six points that lie on the circumference of a circle?
Solution
Since the line that goes from point A to point B is same as the one that goes from B to A, this is a combination problem. It is a combination of 6 objects taken 2 at a time. Therefore, the answer is:
There are 10 people at a party. If they all shake hands, how many hand-shakes are possible?
Solution
Note that between any two people there is only one hand shake. Therefore, we have:
10C2 = 45 hand-shakes.
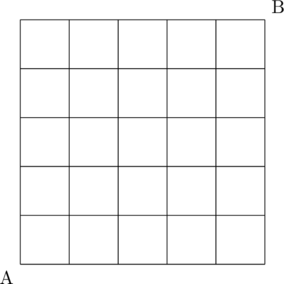
The shopping area of a town is in the shape of square that is 5 blocks by 5 blocks. How many different routes can a taxi driver take to go from one corner of the shopping area to the opposite corner?
Solution
Let us suppose the taxi driver drives from the point A, the lower left hand corner, to the point B, the upper right hand corner as shown in the figure below.
To reach his destination, he has to travel 10 blocks; five horizontal, and five vertical. So if out of the 10 blocks he chooses any five horizontal, the other five will have to be the vertical blocks, and vice versa. Therefore, all he has to do is to choose 5 out of 10:
The answer is 10C5, or 252.
Alternately, the problem can be solved by permutations with similar elements.
The taxi driver’s route consists of five horizontal and five vertical blocks. If we call a horizontal block H, and a vertical block a V, then one possible route may be as follows:
HHHHHVVVVV
Clearly there are
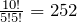
permutations.
Further note that by definition
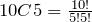
.
If a coin is tossed six times, in how many ways can it fall four heads and two tails?
Solution
First we solve this problem using the permutations with similar elements technique.
We need 4 heads and 2 tails, that is:
HHHHTT
There are
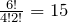
permutations.
Now we solve this problem using combinations.
Suppose we have six spots to put the coins on. If we choose any four spots for heads, the other two will automatically be tails. So the problem is simply:
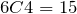
.
Incidentally, we could have easily chosen the two tails, instead. In that case, we would have:
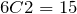
.
Further observe that by definition:
and
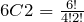
Which implies:
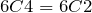
.
Combinations Involving Several Sets
So far we have solved the basic combination problem of r objects chosen from n different objects. Now we will consider certain variations of this problem.
How many five-people committees consisting of 2 men and 3 women can be chosen from a total of 4 men and 4 women?
Solution
We list 4 men and 4 women as follows:
M1M2M3M4W1W2W3W4
Since we want 5-people committees consisting of 2 men and 3 women, we’ll first form all possible two-man committees and all possible three-woman committees. Clearly there are 4C2 = 6 two-man committees, and 4C3 = 4 three-woman committees, we list them as follows:
| 2-Man Committees |
3-Woman Committees |
| M1M2 |
W1W2W3 |
| M1M3 |
W1W2W4 |
| M1M4 |
W1W3W4 |
| M2M3 |
W2W3W4 |
| M2M4 |
|
| M3M4 |
|
For every 2-man committee there are four 3-woman committees that can be chosen to make a 5-person committee. If we choose M1M2 as our 2-man committee, then we can choose any of W1W2W3 , W1W2W4 , W1W3W4 , or W2W3W4 as our 3-woman committees. As a result, we get:
Similarly, if we choose M1M3 as our 2-man committee, then, again, we can choose any of W1W2W3 , W1W2W4 , W1W3W4 , or W2W3W4 as our 3-woman committees.
And so on. Since there are six 2-man committees, and for every 2-man committee there are four 3- woman committees, there are altogether 6 · 4 = 24 five-people committees. In essence, we are applying the multiplication axiom to the different combinations.
A high school club consists of 4 freshmen, 5 sophomores, 5 juniors, and 6 seniors. How many ways can a committee of 4 people be chosen that includes:
a. One student from each class?
b. All juniors?
c. Two freshmen and 2 seniors?
d. No freshmen?
e. At least three seniors?
Solution
a. Applying the multiplication axiom to the combinations involved, we get:
4C1 · 5C1 · 5C1 · 6C1 = 600
b. We are choosing all 4 members from the 5 juniors, and none from the others.
5C4 = 5
c. 4C2 · 6C2 = 90
d. Since we don’t want any freshmen on the committee, we need to choose all members from the remaining 16. That is:
16C4 = 1820
e. Of the 4 people on the committee, we want at least three seniors. This can be done in two ways. We could have three seniors, and one non-senior, or all four seniors:
(6C3 · 14C1) + 6C4 = 295
How many five-letter word sequences consisting of 2 vowels and 3 consonants can be formed from the letters of the word INTRODUCE?
Solution
First we select a group of five letters consisting of 2 vowels and 3 consonants. Since there are 4 vowels and 5 consonants, we have:
4C2 · 5C3
Since our next task is to make word sequences out of these letters, we multiply these by 5!:
4C2 · 5C3 · 5! = 7200.
A standard deck of playing cards has 52 cards consisting of 4 suits each with 13 cards. In how many different ways can a 5-card hand consisting of four cards of one suit and one of another be drawn?
Solution
We will do the problem using the following steps. Step 1. Select a suit. Step 2. Select four cards from this suit. Step 3. Select another suit. Step 4. Select a card from that suit.
Applying the multiplication axiom, we have:
| Ways of selecting a suit |
Ways if selecting 4 cards from this suit |
Ways if selecting the next suit |
Ways of selecting a card from that suit |
| 4C1 |
13C4 |
3C1 |
13C1 |
4C1 · 13C4 · 3C1 · 13C1 = 111,540.
Practice questions
1. How many different 3-people committees can be chosen from 10 people?
2. How many 5-card hands can be chosen from a deck of cards?
3. There are five teams in a league. How many games are played if every team plays each other twice?
4. How many 4-people committees chosen from four men and six women will have at least three men?
5. Three marbles are chosen from a jar that contains 5 red, 4 white, and 3 blue marbles. How many samples of the following type are possible?
a. All three white
b. One of each colour
c. At least two red
6. There are 15 technicians and 11 chemists working in a research laboratory. In how many ways could they form a 5-member safety committee if the committee:
a. Must have exactly one technician
b. Must have two technicians and three chemists
c. Must have at least three chemists
![]()
![]()
![]()
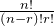 , where n and r are natural numbers.
, where n and r are natural numbers.