5.2. Multiplication Axiom
Multiplication Axiom
In this chapter, we are trying to develop counting techniques that will be used in future chapters to study probability. One of the most fundamental of such techniques is called the Multiplication Axiom. Before we introduce the multiplication axiom, we first look at some examples.
Example 5.2.1
If a student has two shirts and three pairs of pants they want to wear, how many different outfits consisting of these shirts and pants can they wear?
Solution
Suppose we call the shirts s1 and s2, and pants p1, p2, and p3. We can have the following six outfits.
s1p1 , s1p2 , s1p3 , s2p1 , s2p2 , s2p3
Alternatively, we can draw a tree diagram:
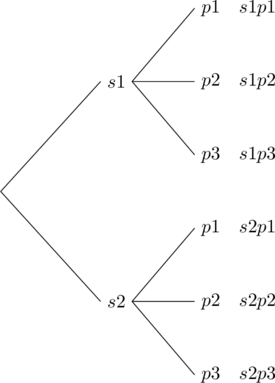
The tree diagram gives us all six possibilities. The method involves two steps. First the student chooses a shirt. They have two choices: shirt one or shirt two. If they choose shirt one, they have three pairs of pants to match it with; pants one, pants two, or pants three. Similarly if they choose shirt two, they can match it with each of the three pairs of pants, again. The tree diagram helps us visualize these possibilities.
The reader should note that the process involves two steps. For the first step of choosing a shirt, there are two choices, and for each choice of a shirt, there are three choices of choosing a pair of pants. So altogether there are 2 · 3 = 6 possibilities.
Example 5.2.2
If a student has two shirts, three pairs of pants, and two pairs of shoes they want to wear, how many different outfits consisting of these items of clothing can they wear?
Solution
Suppose we call the shirts s1 and s2, the pants p1, p2, and p3, and the shoes f1, and f2. The following tree diagram results.
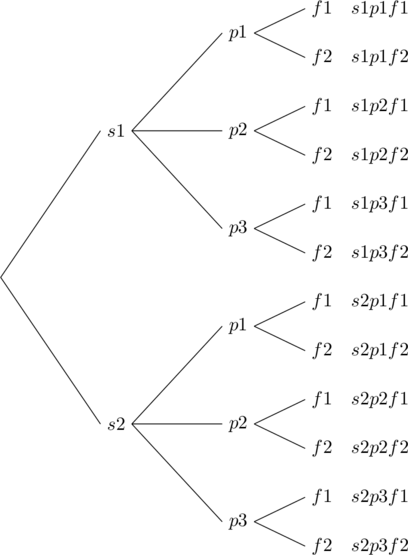
We count the number of branches in the tree, and see that there are 12 different possibilities. This time the method involves three steps. First, the student chooses a shirt. They have two choices: shirt one or shirt two. Now suppose they choose shirt one. This takes us to step two of the process which consists of choosing a pair of pants. They have three choices for a pair of pants, and let us suppose they choose pants two. Now that they have chosen a shirt and pants, we have moved to the third step of choosing a pair of shoes. Since they have two pairs of shoes, they have two choices for the last step. Let us suppose they choose shoes two. They have chosen the outfit consisting of shirt one, pants two, and shoes two, or s1p2f2.
By looking at the different branches on the tree, one can easily see the other possibilities. The important thing to observe here, again, is that this is a three step process. There are two choices for the first step of choosing a shirt. For each choice of a shirt, there are three choices of choosing a pair of pants, and for each combination of a shirt and pants, there are two choices of selecting a pair of shoes. All in all, we have 2 · 3 · 2 = 12 different possibilities.
The tree diagrams help us to visualize the different possibilities, but they are not practical when the possibilities are numerous. Besides, we are mostly interested in finding the number of elements in the set and not the actual possibilities. But once the problem is envisioned, we can solve it without a tree diagram. The two examples we just solved may have given us a clue to do just that. Let us now try to solve the previous example without a tree diagram. Recall that the problem involved three steps: choosing a shirt, choosing a pair of pants, and choosing a pair of shoes. The number of ways of choosing each are listed below.
| The number of ways of choosing a shirt | The number of ways of choosing pants | The number of ways of choosing shoes |
| 2 | 3 | 2 |
By multiplying these three numbers we get 12, which is what we got when we did the problem using a tree diagram. The procedure we just employed is called the multiplication axiom.
The Multiplication Axiom: If a task can be done in m ways, and a second task can be done in n ways, then the operation involving the first task followed by the second can be performed in m · n ways.
The general multiplication axiom is not limited to just two tasks and can be used for any number of tasks.
Example 5.2.3
| Letter | Digit | Digit | Digit | Digit |
| 26 | 10 | 10 | 10 | 10 |
Therefore, the number of possible license plates is 26 · 10 · 10 · 10 · 10 = 260,000.
Example 5.2.4
| Question 1 | Question 2 | Question 3 |
| 2 | 2 | 2 |
Applying the multiplication axiom, we get 2 · 2 · 2 = 8 different ways.
Example 5.2.5
| 4 | 3 | 2 | 1 |
So there are altogether 4 · 3 · 2 · 1 = 24 different ways.
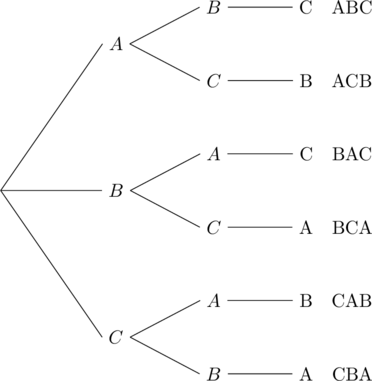
Example 5.2.6
| 3 | 2 | 1 |
Therefore, 6 different word sequences can be formed.
Practice questions
1. A license plate consists of three letters followed by three digits. How many license plates are possible if no letter may be repeated?
2. How many seven-digit telephone numbers are possible if the first two digits cannot be ones or zeros?
3. In how many ways can a 4-question true-false test be answered?
4. How many different ways are possible to answer an exam with 8 multiple-choice questions containing 4 answer options, and 7 true-false questions?
5. You want to create a new password for your phone consisting of 4 numbers (0-9), but you don’t want to reuse the same number more than once. How many different password possibilities are there?
6. A combination lock is opened by first turning to the left, then to the right, and then to the left again. If there are 30 digits on the dial, how many possible combinations are there?

